Description

In this project, I wrote a software that plans a trajectory for the end-effector of the YouBot mobile manipulator, performs an odometry as the chassis moves, and performs feedback control to drive the youBot to pick up a block at a specified location, carry it to a desired location, and put it down in the V-REP simulation software.

The YouBot is an omnidirectional mobile robot with a 5-DOF robotic arm, simulated in CoppeliaSim simulation software.

Take a look at the project on my GitHub page.

For further information about this project, visit the project's Wiki page.

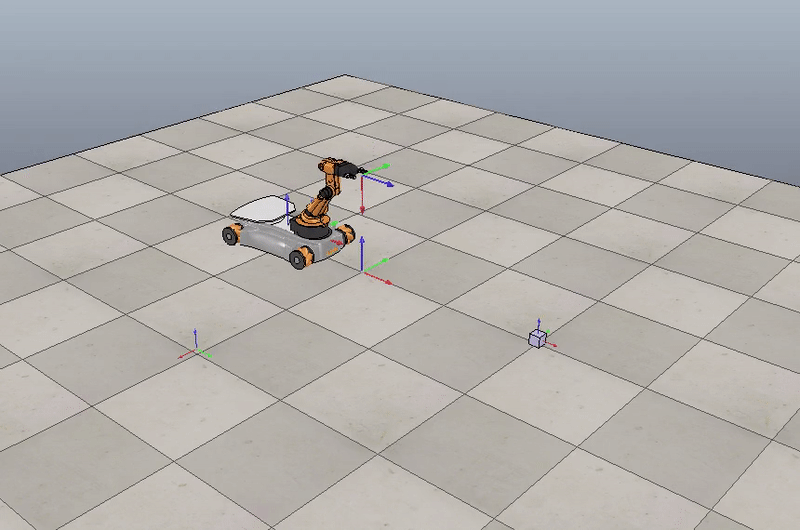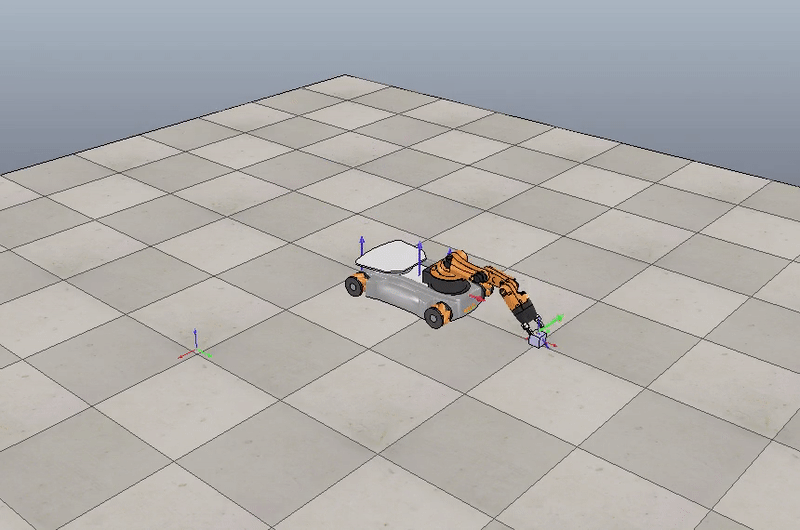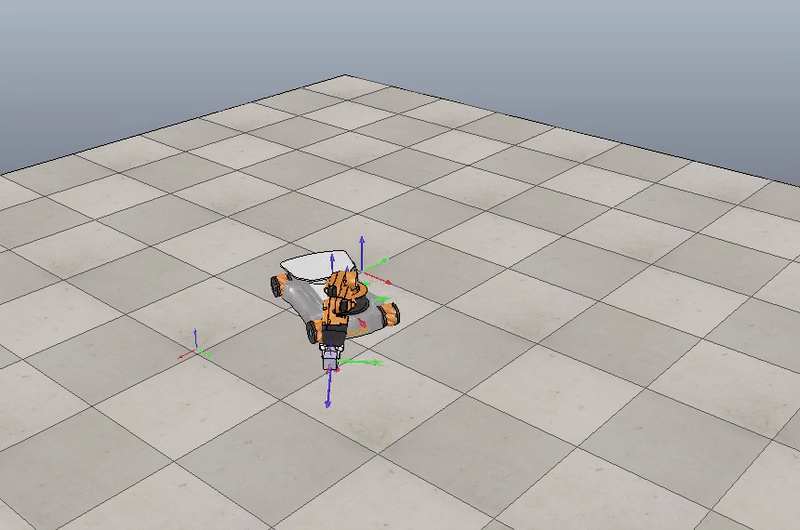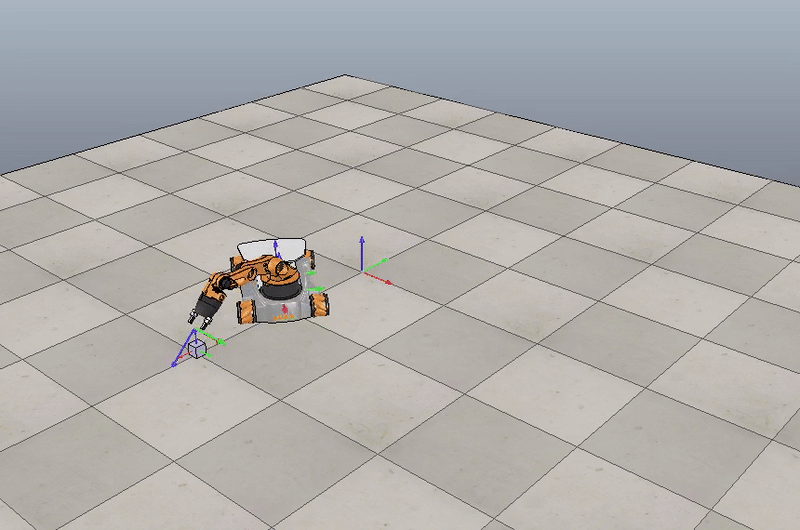
Motion planning for YouBot mobile manipulator

Overview

The project covers the following topics:

Generating the Kinematics Simulator of the YouBot

In this part of the project, I wrote a code that computes the next configuration of the robot, given joints and wheels speed, and current robot configuration: $$ q = \begin{bmatrix} \phi_{chassis} \\ x_{chassis} \\ y_{chassis} \\ J_1 \\ J_2 \\ J_3 \\ J_4 \\ J_5 \\ W_1 \\ W_2 \\ W_3 \\ W_4 \\ Gripper \end{bmatrix} $$

In this part I also applied restriction on the robot's velocity.

Planning the End-Effector's Trajectory

In this part of the project, I wrote a code that generates a reference trajectory for the robot's end-effector, given the end-effector configuration in different states, relative to the world or the cube frame.

I find the configurations along the robots path, as it goes through several waypoints:

1. Starts from rest in initial position
2. From initial position to standoff position (near the cube position)
3. From standoff position to grasp position
4. Closing the gripper
5. From grasp position to standoff position (near the cube goal position)
6. From standoff position to goal position
7. From goal position to final position
8. opening the gripper
9. From final position to standoff position

Applying Feedback Control to Drive the Robot in the Desired Trajectory

In this part of the project, I wrote a code that returns the commanded end-effector twist and the error of each joint, given the current, desired and next end-effector configurations and the PI control gains.

The feedback control of the the mobile manipulator is given by kinematic task-space feedforward plus feedback control law: $$ \nu(t) = [Ad_{X^{-1}X_d}]\nu_d(t) + K_pX_{err}(t) + K_i\int_0^t X_{err}(t)dt $$

Results

Motion Planning with Different Initial and Final Cube Position

In this part, I simulated the the controlled motion with different initial and final cube position, and different initial robot's configuration.

Here is a motion planning and control simulation for a different cube position:

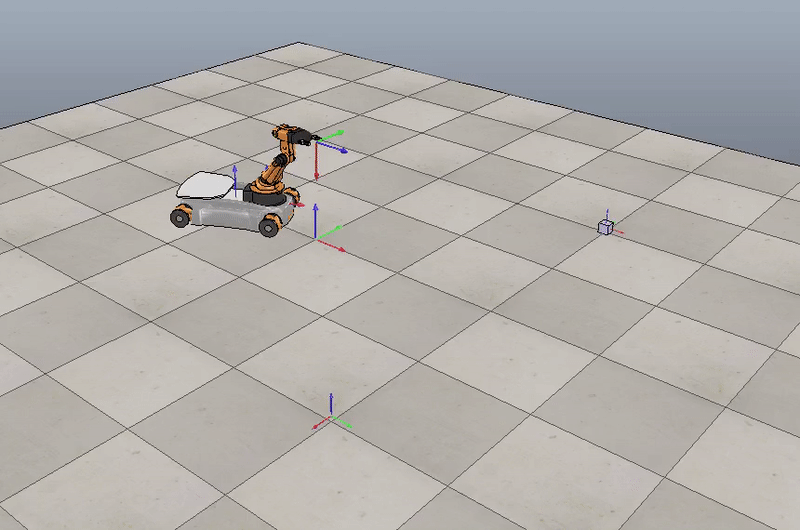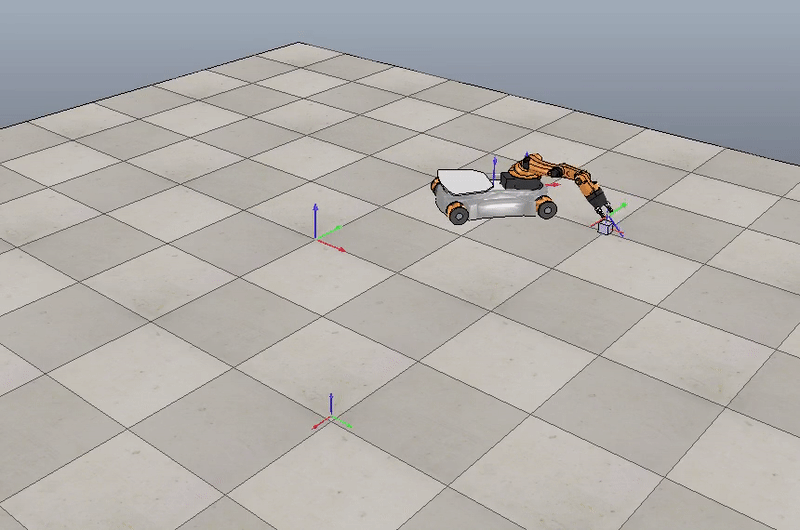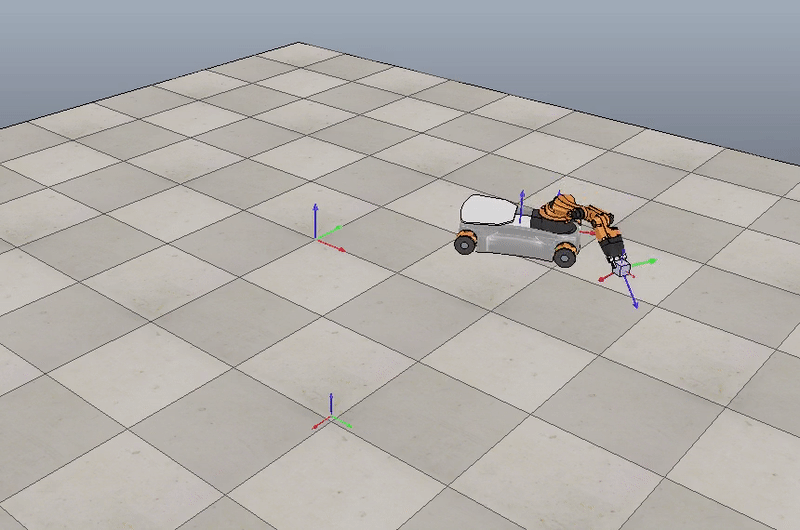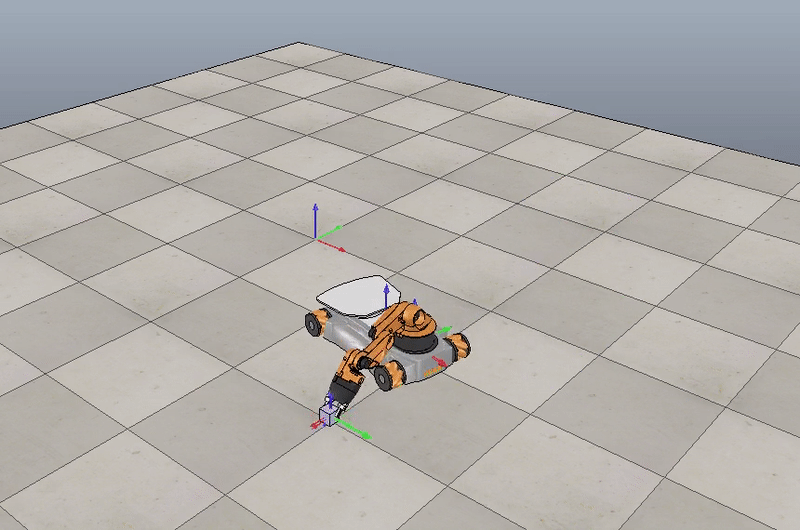
Initial position $(1, 1, 0)$, Final position $(1, -1, \frac {\pi}{2})$

Motion Planning with Different Control Gains

In this part, I plotted the end-effector's twist error as a function of time, to explore the error's behavior when using different control gains.

Here are two motion planning and control simulations for different control gains:

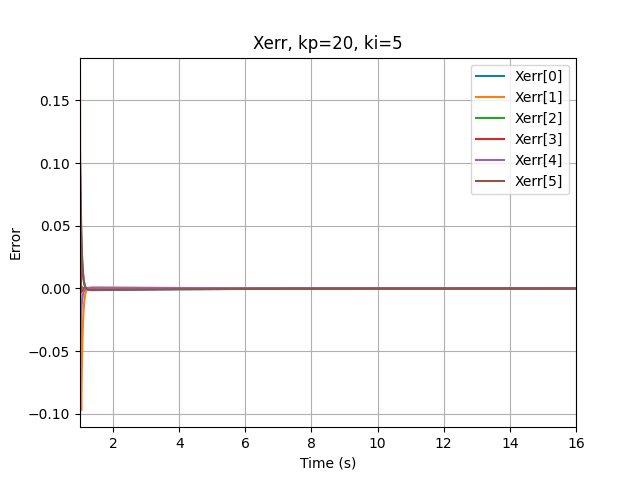
$k_p=20, k_i=5$ - Controlled motion

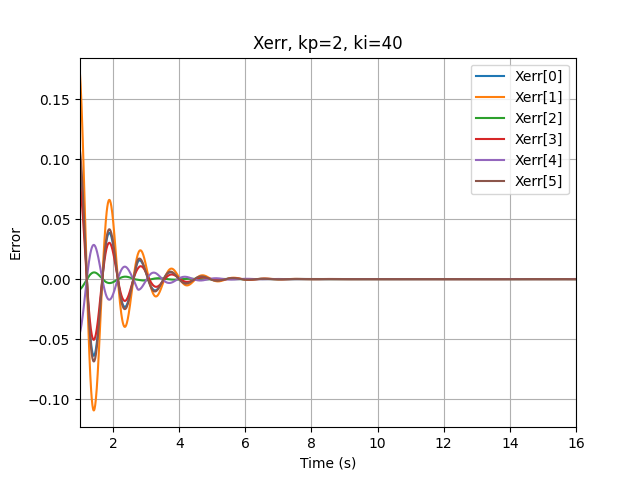
$k_p=2, k_i=40$ - Overshoot motion